Konsep Turunan - Asal-Usul Turunan

http:

Hai hai semua . Ketemu lagi sama aing, Admin K yang kece lagi keren . Tentu saja, masih di blog kesayangan qta yang indah ini, KnK Land. Kali ini aing bakal ngebahas tentang turunan. Apa sih itu turunan? Kebanyakan siswa atau mahasiswa khususnya yang ada matematikanya pasti pernah mendengar apa yang dinamakan turunan. Mereka juga bisa menyelesaikan soal turunan dengan mudahnya. Namun, banyak juga dari mereka yang meski bisa mengerjakan soal tapi gak tau apa itu turunan. Nah, untuk mengurangi populasi robot matematika, aing akan menjelaskan tentang konsep turunan ini. Langsung saja, cekidoot .

Tama2 mari qta bahas tentang fungsi dan kurva. Suatu fungsi dapat digambarkan dalam koordinat kartesius sehingga dapat membentuk kurva. Misalnya aing punya kurva f(x) sebagai berikut.

Nah itulah contoh dari kurva. Untuk sekarang, qta tinggalkan kurva itu disini yah.

Mari qta bahas dulu tentang kemiringan suatu garis. Seperti yang qta ketahui bahwa persamaan linear atau garis lurus dapat dituliskan dalam bentuk y = mx + n, dan m merupakan kemiringannya. Apa sih yang dimaksud dengan kemiringan itu?

Kemiringan dari suatu garis didefinisikan sebagai seberapa cepat kenaikan atau penurunan tinggi dari titik asal pada garis apabila digeser dari kiri ke kanan (apabila nilai x-nya naik dalam koordinat kartesius). Perhatikan beberapa bola dan garis miring yang berupa tanjakan berikut ini.

Perhatikan bahwa bola tersebut mau berjalan dari kiri ke kanan. Semakin ke kanan, maka bola2 tersebut akan semakin tinggi. Dapat dilihat bahwa bola yang ke-3 akan cepat meninggi dari pada bola yang lain apabila kecepatan dari kiri dan kanannya itu sama. Qta sebut saja garis yang membuat bola naik ini adalah garis yang memiliki kemiringan positif.

Sebaliknya, kalo bolanya turun, qta bisa sebut sebagai garis yang mempunyai kemiringan negatif.

Lalu, bagaimana cara menghitung kemiringan dari suatu garis? Kemiringan suatu garis dapat didefinisikan sebagai perubahan ketinggian dibagi jarak dari kiri ke kanan. Misalnya ketinggian awal adalah y0, ketinggian akhir adalah y, dan jaraknya adalah ∆x, maka

Yang di atas itu bolanya naik. Tentu jika bolanya turun maka y0 > y, menghasilkan y - y0 negatif sehingga mengakibatkan kemiringannya  menjadi negatif.

Kemiringan juga biasa disebut gradien. Menghitung gradien dari garis lurus memang sangatlah mudah. Namun, bagaimana mencari kemiringan dari kurva yang melengkung lengkung? Mari qta ambil kurva yang di atas.

Lihatlah kurva ini wahai sahabatque. Kurva ini melengkung dan gak lurus. Jika qta perhatikan ada yang menanjak dan ada yang turun. Ada yang menggunung, ada juga yang melembah. Jika qta lihat dari x = 0 sampe x = 2, tentu kenaikan kurva relatif lebih lambat dibandingkan dengan dari x = 5 sampai x = 7. Bahkan kenaikan dari setiap titik2 pada kurva dari x = 0 sampai x = 2 itu berbeda2 sahabatque. Karena setiap titik2 memiliki nilai 'kemiringan' yang berbeda2, maka qta hanya bisa mencari kemiringan dari satu titik aja guys. Lalu, bagaimana cara mencari kemiringan dari suatu titik? Yang bisa qta lakukan hanya menggunakan pendekatan sahabatque.

Mungkin fungsi di atas agak susah guys, mending aing kasih fungsi yang agak familiar gitu deh. Misalnya fungsi f(x) = x². Berikut, gambarnya.

 
Sekarang, aing mau mencari kemiringan pada titik (1,1). Untuk mencarinya, qta harus mendekatinya dengan suatu garis.

Masih kurang puas? Mari kecilkan garisnya lagi! Mari qta dekatkan bagian bawahnya ke arah 1.

Sepertinya kemiringannya sudah cukup dekat. Mari qta masukan rumus kemiringan.

Untuk bisa mendapatkan kemiringan pada titik tersebut, qta harus memilih ∆x cukup dengan dengan x = 1. Nilai y dan y0 bergantung pada nilai x dan ∆x beserta fungsinya. Itu artinya y = f(x + ∆x), sedangkan y0 = f(x). Itu artinya rumusnya bisa diubah menjadi seperti berikut.

Tentu, semakin kecil nilai ∆x maka akan semakin akurat qta bisa mendapatkan kemiringan atau gradien pada titik tersebut. Jika qta memilih ∆x = 0 tentu tidak bisa. Lalu, bagaimana jika qta memilih bilangan yang sangat2 kecil mendekati 0? Berarti, ini waktunya qta harus menggunakan limit!

Dan ketahuilah bahwa inilah definisi dari turunan suatu fungsi . Mencengangkan bukan?

Dengan mengetahui turunannya, qta bisa mengetahui gradien dari garis singgung yang memotong pada suatu titik pada suatu fungsi. Adapun untuk pembahasan lebih lanjut lagi, bakal aing bahas di postingan laen kali. Perlu diingat bahwa turunan itu sendiri adalah merupakan proses limit. Jadi, kalo ditanya mana lebih dulu turunan atau limit tentu jawabannya adalah limit. Jadi sebelum belajar turunan, alangkah baiknya belajar limit terlebih dahulu.

Skarang mari, qta lanjutkan soal yang tadi. Tentu, aing udah kasih tau kalo fungsinya itu f(x) = x². Mari qta turunkan fungsi ini.

Masukkan ke rumus



Setelah itu, qta evaluasikan.

Lalu, qta coret yang enak dicoret

Qta faktorkan, keluarkan ∆x-nya.

Next, tentu saja, qta cancel out alias corat coret.

Qta ketahui bahwa ∆x mendekati nol, itu artinya 2x + ∆x menuju ke 2x. Berarti

Pada titik (1,1) kemiringannya

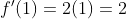
Okeh, sekian pembahasan aing tentang turunan. Semoga memberikan manfaat bagi qta semua. Kalo ada yang kurang paham, alangkah baiknya kasih tau di komeng. Kalo ada kesalahan, mohon diprotes di komeng. Sampai jumpa di postingan berikutnya. Bye~.