Sedikit Pembuktian Aturan L'Hôpital

by Admin K on Saturday, December 28, 2019 in Matematikamampus

Hai hai semua

. Ketemu lagi sama aing, Admin K yang pinter lagi sehat

. Tentu saja, masih di blog yang penuh dengan imajinasi dan pertumbuhan ini, KnK Land. Kali ini, aing akan membahas lagi tentang matematika terutama mengenai dunai perlimitan kalkulus. Nah, pada postingan kali ini, aing akan membahas tentang aturan L rumah sakit atau L'Hôpital (kira-kira dibaca "el hospital"). Sesuai judul, aing akan membahas tentang aturan ini secara khusus untuk situasi 0/0 makanya dalam judul aing menggunakan kata "sedikit". Hal ini aing lakukan agar iman kalian bertambah kuat terhadap aturan instan ini. Baiklah, langsung saja, kita cekidoot dulu geys
.

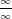
L'Hôpital adalah alat yang powerful yang digunakan dalam penyelesaian persoalan limit. Tak heran aturan ini diajarkan di SMA dan berbagai tempat les persiapan ujian. Aturan L'Hôpital sangat berguna untuk menyelesaikan persoalan limit bentuk tak tentu (indeterminate form) seperti bentuk $\frac{0}{0}$ dan bentuk $\frac{\infty}{\infty}$ . L'Hôpital menggunakan turunan untuk menyelesaikan persoalan limit dari pembagian fungsi.

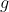
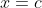
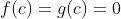
Okay, mari kita mulai pembuktiannya untuk kasus khusus situasi $\frac{0}{0}$ . Jadi misalkan ada dua fungsi yakni $f$ dan $g$ yang masing-masing mempunyai turunan di titik $x=c$ , dengan $f(c)=g(c)=0$ dan $g'(c)\neq0$ .

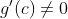
Nah, masalahnya sekarang adalah mencari limit dari pembagian kedua fungsi tersebut yakni
$\lim_{x\rightarrow c}\frac{f(x)}{g(x)}$

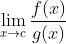
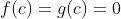
Jelas bahwa ini adalah situasi $\frac{0}{0}$ sebab telah diketahui bahwa $f(c)=g(c)=0$ . Nah, untuk membuktikan kebenaran aturan L'Hôpital pada situasi ini, tidak masalah kan kalau pembilang dan penyebutnya dikurangi 0 karena sama saja? Sehingga diperoleh

$\lim_{x\rightarrow c}\frac{f(x)}{g(x)}=\lim_{x\rightarrow c}\frac{f(x)-0}{g(x)-0}$

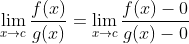
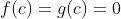
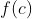
Ingat bahwa $f(c)=g(c)=0$ . Kita ganti 0 pada pembilang dengan $f(c)$ , dan 0 pada penyebut dengan $g(c)$ . Sehingga diperoleh
$\lim_{x\rightarrow c}\frac{f(x)}{g(x)}=\lim_{x\rightarrow c}\frac{f(x)-f(c)}{g(x)-g(c)}$

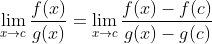
Ingat bahwa $x$ hanya mendekati $c$ , itu berarti $x-c\neq0$ . Jadi, kita boleh mengalikan ekspresi limit tersebut dengan
$\frac{(\frac{1}{x-c})}{(\frac{1}{x-c})}=1.$

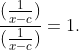
Sehingga diperoleh
$\lim_{x\rightarrow c}\frac{f(x)}{g(x)}=\lim_{x\rightarrow c}\frac{f(x)-f(c)}{g(x)-g(c)}\cdot \frac{(\frac{1}{x-c})}{(\frac{1}{x-c})}$

$\lim_{x\rightarrow c}\frac{f(x)}{g(x)}=\lim_{x\rightarrow c}\frac{(\frac{f(x)-f(c)}{x-c})}{(\frac{g(x)-g(c)}{x-c})}.$

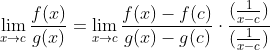
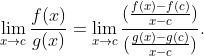
Dengan aturan limit untuk pembagian, limitnya bisa dipecah ke pembilang dan penyebut, diperoleh
$\lim_{x\rightarrow c}\frac{f(x)}{g(x)}=\frac{(\lim_{x\rightarrow c}\frac{f(x)-f(c)}{x-c})}{(\lim_{x\rightarrow c}\frac{g(x)-g(c)}{x-c})}.$

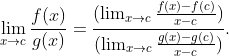
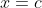
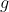
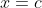
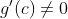
Perhatikan pembilang dan penyebut, itu tidak lain adalah definisi turunan fungsi di titik $x=c$ . Mengingat $f$ dan $g$ yang masing-masing mempunyai turunan di titik $x=c$ dan $g'(c)\neq0$ , persamaan menjadi

$\lim_{x\rightarrow c}\frac{f(x)}{g(x)}=\frac{f'(c)}{g'(c)}.\blacksquare$

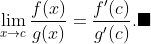
Yap, cukup sekian pembuktiannya

. Keren, bukan? Ini hanya membuktikan kasus khusus L'Hôpital yakni situasi $\frac{0}{0}$ saja dengan turunan penyebutnya $g'(c)\neq0$ .

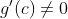
Okay, cuma tambahan dikit. Sebagai contoh mari kita selesaikan limit berikut ini.

$\lim_{x\rightarrow 0}\frac{e^x-1}{x}$

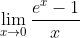
Dengan L'Hôpital yang udah kita buktikan tadi, dan mengingat turunan fungsi eksponensial adalah dirinya sendiri, diperoleh

$\lim_{x\rightarrow 0}\frac{e^x-1}{x}=\frac{e^0}{1}=1.$

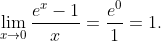
Wah, mudah bingits bukan?? Yap, cukup sekian postingan dari aing. Kalo ada kesalahan atau ada yang kurang, silakan sampekan di komeng. Sampe jumpa di postingan selanjutnya, bye~