Graf Euler

Hai hai semua . Ketemu lagi sama aing, Admin K yang kece lagi keyen . Tentu saja, masih di blog kesayangan kita yang penuh dengan cinta dan kebahagiaan ini, KnK Land. Kali ini aing akan menjelaskan salah satu materi dalam matematika diskrit yakni teori graf. Graf yang bakal aing bahas kali ini adalah salah satu graf sepesial yaitu graf Oylah Euler. Langsung saja kita cekidoot ke postingan utamanya geys .




Sebelum membaca postingan ini, alangkah baiknya kalian sudah mempelajari tentang konsep graf, apa itu graf, konsep ketetanggaan, dll mengenai dasar-dasar graf atau bagian kulit materi teori graf. Atau, kalau kalian mau memaksakan diri untuk membaca postingan ini, ya gak masalah juga sih.

Pendahuluan

Sebagai pembukaan, perhatikan gambar berikut.

Itu adalah peta Kota Koniker Königsberg (sekarang bernama Kaliningrad). Pada peta tersebut, terdapat 7 buah jembatan yang ditandai dengan warna merah. Nah, kota ini adalah kota lejen karena sering dibahas pada saat pertama kali belajar teori graf. Oke oke, kembali ke pembicaraan. Perhatikan gambar tersebut. Kota Königsberg terdiri atas 4 area yang dihubungkan oleh jembatan-jembatan. Jalan-jalan di kota tersebut memang bisa sangat melelahkan. Nah, bicara soal jalan-jalan, apakah mungkin kita melewati tiap jembatannya masing-masing satu kali hanya dengan sekali jalan saja? Ini adalah pertanyaan yang muncul dari para penduduk di kota itu pada abad ke-18.

Teka-teki ini pun menjadi perbincangan bagi para matematikawan termasuk primadona dari postingan ini, Leonhard Euler. Dia ternyata bisa menyelesaikan permasalahan ini dengan mudah dengan teori graf. Wow! Jawaban yang dia peroleh dengan menggunakan teori graf adalah "Tidak bisa!". Wow, jawaban yang sangat fantastis, bukan? Kalau seandainya memang bisa, maka kita tinggal memberikan contoh jalur yang mana jembatan yang harus dilewati terlebih dahulu. Namun, faktanya memang tidak bisa.

Lalu, bagaimana caranya mas Oylah Euler memecahkan teka-teki ini dengan teori graf? Hmm, menarik sekali bukan? Oke-oke. Sebelum itu, aing masih mau kasih  teka-teki lagi. Apakah kalian bisa menggambar gamber berikut hanya dengan satu kali coretan tanpa mengangkat pensil/pulpen dengan tidak melewati jalur yang sama dua kali?

Silakan kalian kotret-kotret di kertas kalian, coba gambar pola tersebut hanya dengan sekali menggaris tanpa mengangkat pensil/pulpen. Pasti kalian bisa menyelesaikannya dengan mudah. Nah, bagi kalian yang penasaran, berikut solusinya.

Nah, tantangan berikutnya, coba deh gambar yang ini dengan cara yang sama yakni cuma sekali garis.

Nah, yang ini meskipun lebih "besar"/"panjang" daripada pola sebelumnya, sebenarnya ini lebih mudah dicari solusinya karena solusinya lebih banyak dibandingkan pola sebelumnya. Kenapa solusinya lebih banyak? Karena penggambaran pola yang kedua ini bisa dimulai dari titik manapun. Sedangkan, yang sebelumnya, hanya bisa dimulai dari titik tertentu lalu berhenti di titik tertentu. Lah, darimana aing tau? Ya, tentu saja aing tau karena udah belajar teori graf. Konsep yang digunakan untuk bisa menebak dari awal, mana pola yang bisa digambar dengan sekali coret, mana yang solusinya banyak, ataupun mana yang solusinya cuma dua adalah dengan menggunakan konsep graf Euler.

Graf Euler

Apa itu graf Euler? Graf Euler adalah graf yang mempunyai lintasan tertutup/sirkuit euler. Apa itu sirkuit Euler? Sirkuit Euler pada suatu graf adalah sirkuit yang memuat semua sisi-sisi dari graf tersebut. Contohnya pola di atas bisa dibuat graf sebagai berikut.

Selanjutnya, alangkah baiknya titik-titiknya diberikan label yah lur.

Nah, pada graf tersebut, kita bisa menemukan lintasan-lintasan/sirkuit-sirkuit Euler. Misalnya saja a-b-c-d-e-f-c-e-b-d-a.

Jadi, benar bahwa, graf tersebut adalah graf Euler sebab mempunyai sirkuit Euler.

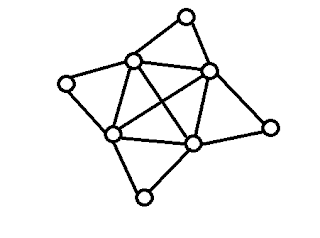
Mari kita coba graf yang lain. Misalnya saja graf berikut, apakah graf berikut mempunyai sirkuit Euler?

Tantangan untuk kalian, silakan kotret-kotret di kertas dan cari lintasan Eulernya. Apakah kalian bisa menemukan lintasan tertutup yang memuat semua sisi di graf ini? Jawabannya adalah tidak. Mau sampai kapanpun kalian mencoba bahkan sampai 18 juta tahun pun, kalian tidak akan bisa menemukan sirkuit Euler di graf ini. Darimana bisa diketahui kalau graf ini bukan graf Euler? Tentu, kita harus tau ilmunya terlebih dahulu. Sebenarnya sangat mudah menebak mana graf Euler dan mana bukan graf Euler.

Coba perhatikan deh, saat kita membuat suatu sirkuit Euler, pastinya kita akan melewati sebuah titik. Saat kita melewati sebuah titik selain titik awal, maka kita juga harus keluar lagi. Sebab, kalau tidak keluar lagi, maka kita tidak bisa melanjutkan perjalanan.

Nah, setiap kali kita melewati/masuk ke suatu titik (bisa saja titik awal dilewati lagi), pastinya kita akan pergi lagi. Adapun karena titik awal sama dengan titik akhir, maka titik awalnya juga harus berderajat genap sebab kalau kita pergi dari titik awal maka kita harus kembali lagi. Itu tandanya apa? Itu tandanya bahwa titik yang kita lewati harus mempunyai derajat genap atau banyak sisi yang terkait haruslah genap.

Sekarang perhatikan kembali graf impossible tadi yang kalian coba-coba cari lintasan Eulernya tapi gak bisa.

Tampak jelas bahwa ada titik-titiknya yang berderajat ganjil yakni berderajat 5.

Lihat, ada 4 titik yang berderajat 5. Hal ini menunjukkan bahwa, kita tidak bisa membuat lintasan/sirkuit Euler pada graf tersebut.

Euler menyatakan bahwa, suatu graf mempunyai lintasan Euler jika dan hanya jika setiap titiknya berderajat genap. Dengan kata lain, setiap graf yang semua titik-titiknya berderajat genap adalah graf Euler. Dari atas, kita sudah ketahui bahwa, semua titik berderajat genap adalah syarat perlu agar suatu graf menjadi graf Euler. Selanjutnya dapat dibuktikan bahwa semua graf yang titik-titiknya berderajat genap pasti adalah graf Euler. Buktinya tidak aing cantumkan disini maaf yak soalnya inti dari postingan ini bukan membuktikan cuma nambah wawasan aja atau menambah  ketertarikan pada teori graf.

Baiklah, mari kita kembali ke jembatan Koniker Königsberg. Apakah kita bisa melewati setiap jembatan hanya dengan sekali lewat? Hmm.

Kita bisa memodelkan kota Königsberg ke dalam bentuk graf. Keempat area yang terpisah kita wakili dengan titik, sedangkan ketujuh jembatan bisa kita wakili dengan sisi. Suatu sisi akan terkait dengan suatu titik apabila sisi tersebut diwakili oleh jembatan yang menghubungkan area yang diwakili titik tersebut.

Coba perhatikan ternyata setelah dimodelkan menjadi graf, rupanya titik-titiknya berderajat ganjil. Itu artinya kita tidak bisa membuat lintasan Euler dari graf tersebut. Dengan kata lain, kita tidak bisa melewati setiap sisi graf (jembatan) hanya dalam sekali lewat. Yap, masalah jembatan di kota Königsberg sudah terpecahkan.

Oh yah, kita juga bisa melewati setiap sisi pada graf meskipun bukan graf Euler yakni hanya ketika cuma ada 2 buah titik yang berderajat ganjil. Namun, posisi awal dan akhirnya harus pada titik yang berderajat ganjil. Contohnya saja graf-graf berikut. Kita bisa berjalan dari titik merah ke titik merah lain dengan melewati setiap sisi masing-masing satu kali. Graf-graf tersebut dinamakan graf Semi-Euler.

Perbedaannya dengan graf Euler adalah saat kita melakukan "perjalanan" (harus melewati setiap sisi masing-masing satu kali) dari suatu ke titik lain pada graf Semi-Euler, kita harus memulai dari titik yang berderajat ganjil lalu berakhir di titik yang berderajat ganjil yang lain. Sedangkan, pada graf Euler kita bisa mulai dari titik mana saja kemudian kembali lagi ke titik awal.

Baiklah, cukup sekian pembahasan aing tentang graf Euler. Semoga bermanfaat bagi kita semua. Kalau ada pertanyaan, tambahan, atau protes, silakan curahkan semua unek-unek di kolom komentar. Sampai jumpa di postingan selanjutnya. Bye~