Hai hai semua ^_^ Aye Admin K. Kali ini aye akan membuktikan salah satu identitas trigonometri. Kok bisa yah sin² x + cos² x = 1? Bahkan ini berlaku untuk setiap besar sudut x. Kok bisa yah? Berikut buktinya.
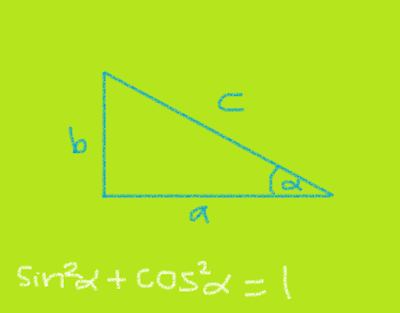
Misal kita punya segitiga siku-siku, yang salah satu sudut nonsiku-sikunya adalah 𝛳. Gambarnya adalah sebagai berikut.
Lanjut, kita namai semua panjang sisi-sisinya.
Selanjutnya, kita nyatakan sin 𝛳 dan cos 𝛳 dengan variabel panjang sisi yang kita buat.
Kita kuadratin diperoleh
Nah, tinggal kita jumlahkan kedua-duanya
Selanjutnya, ingat teorema Pythagoras a² + b² = c².
Terbukti.
Nah, gimana? Paham? Bdw, bukti dengan gambar ini hanya berlaku untuk 0° < 𝛳 < 90° ya karena memang yang digambar adalah 𝛳 sudut lancip. Untuk 90° ≤ 𝛳 ≤ 360°, silakan kalian pikirin sendiri buktinya yah, muehehe.
OH YAH. Fun fact: sebenarnya ada bukti lain yang tidak perlu menggunakan teorema Pythagoras bahkan teorema Pythagoras itu sendiri bisa dibuktikan menggunakan identitas ini. Mungkin bukti seperti itu bakal aye post lain kali, hehe.
Oke, cukup sekian postingan dari aye kali ini. Kalo ada tambahan, sanggahan, protes, pertanyaan, maupun unek-unek, silakan sampaikan di kolom komentar. Sampai jumpa di postingan selanjutnya. Bye~😃















No comments:
Post a Comment